Закон синусов, который также иногда называют правилом синусов, является одним из самых полезных математических законов при решении треугольников. С его помощью можно легко найти как неизвестные углы, так и неизвестные стороны, и он работает для любого треугольника. Этот простой математический закон гласит: a/sin A = b/sin B = c/sin C.
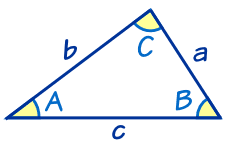
Некоторые студенты, возможно, сейчас почесывают голову и думают: «Это просто?». После того, как он будет разобран на простые слова, ответ будет положительным! Посмотрите на график выше, но обратите внимание, что углы и стороны могут иметь любые измерения, и это может быть любой треугольник. Теперь взгляните на закон. Числители «a», «b» и «c» — это все стороны. Знаменатели «A», «B» и «C» — это соответствующие противоположные углы. Таким образом, если разделить сторону треугольника «a» на синус противоположного угла «A», то результат будет равен стороне «b», деленной на синус «B», а также стороне «c», деленной на синус «C». Видите? Не так сложно, как кажется.
Как использовать закон синусов
Если даны любой угол и соответствующая ему противоположная сторона треугольника, а также сторона или угол другой стороны, то с помощью закона синусов легко найти недостающую информацию. Лучший способ понять, как это сделать, — попробовать на примере. Посмотрите на треугольник ниже. Мы собираемся найти сторону «c», используя полученные знания.
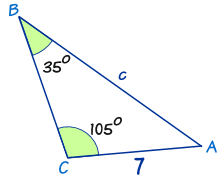
Первым делом необходимо определить, какие соответствующие угол и сторона уже даны. В данном случае угол B, равный 35o, и соответствующая ему сторона b, равная 7, являются нашей единственной отправной точкой. Следующий шаг — подставить все эти числа в приведенное выше уравнение, чтобы определить, какой информации не хватает. Оно будет выглядеть так: a/sin A = 7/sin(35o) = c/sin(105o).
Мы собираемся решить для стороны «c».
Основы алгебры говорят нам, что нужно перестроить уравнение, чтобы выделить переменную, для которой мы решаем. Для целей данного примера полностью проигнорируйте «a/sin A», так как она не несет никакой полезной информации. Для выделения переменной «c» необходимо умножить обе стороны уравнения на sin(105o), в результате мы получим: c = (7/sin(35o)) x sin(105o).
Далее замените значения для sin B и sin C числовыми оценками. Синус 35o приблизительно равен 0,574, а синус 105o можно оценить в 0,966. В результате мы получим c = (7/0,574) x 0,966, или 11,8, если округлить до первого десятичного знака.
Точно такой же процесс можно использовать и для решения неизвестных углов. Просто найдите угол и соответствующую сторону с известными значениями, а также угол, для которого решается задача. Введите их в вышеприведенное уравнение, изолируйте переменную и переверните синус, чтобы получить окончательный ответ.
Решение для другой неизвестной стороны или угла требует еще одного базового знания: все углы в любом треугольнике всегда равны 180o. Учитывая этот важный факт, мы можем просто вычесть два известных угла из 180o, чтобы найти третий, подставить эту информацию в уравнение, как указано выше, и найти последнюю сторону.