Закон косинусов

Закон косинусов, который иногда называют просто правилом косинусов, может быть очень полезен при решении неизвестных сторон и углов во всех типах треугольников. Математик запишет его так: c2 = a2 + b2 — 2abcos(C). Просто, правда? Дальнейшие объяснения не нужны, идем дальше.

Шутка! Хотя среднестатистический математик имеет обширную практику в применении закона косинусов, непосвященному может показаться, что эта череда букв и экспоненты слишком сложна для обработки. Давайте разложим его по полочкам и попробуем разобраться в нем.

Опытные студенты могут вспомнить, что теорема Пифагора, которую можно использовать для вычисления величин прямоугольных треугольников, гласит a2 + b2 = c2. Правило косинусов можно рассматривать как продолжение этой теоремы. Однако, в отличие от открытия Пифагора, этот математический закон справедлив для всех треугольников, а не только для тех, которые включают прямые углы. Он наиболее полезен для нахождения одной недостающей стороны, когда известен соответствующий ей противоположный угол и две другие стороны, или когда известны все стороны. Его также можно просто и эффективно использовать для нахождения углов треугольника, в котором известны все три стороны. Давайте рассмотрим несколько примеров, чтобы понять, почему.

Пример №1: Нахождение неизвестной стороны

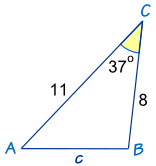
В этом примере известны две стороны и угол, который лежит между ними. Третья сторона, «c», неизвестна. К счастью, закон косинусов отлично подходит для решения задачи с неизвестной переменной; однако если бы мы решали задачу для «a», то нам пришлось бы сделать дополнительный шаг — выделить переменную, прежде чем продолжить. Поскольку «c2» уже выделена с одной стороны уравнения, все, что нам нужно сделать, это подставить известные значения. После этого уравнение будет выглядеть так: c2 = 82 + 112 — 2(8)(11)cos(37o).

Не забывайте соблюдать порядок действий при выполнении этих вычислений. Во-первых, все экспоненты можно вычислять независимо друг от друга, чтобы получить 64 и 121 для a2 и b2. Для решения уравнения косинус 37o может быть приближен численно к 0,798, что приводит к уравнению следующего вида: c2 = 64 + 121 — 176 x 0,798, или c2 = 44,44. Разумеется, это только приближение.

Если ситуация требует большей точности, оцените число до последующих десятичных знаков. Наконец, взяв квадратный корень из обеих сторон, мы получим c = 6,67.

Этот же процесс можно использовать для нахождения любого угла в треугольнике, если известны все три стороны.

Когда формула используется для вычисления недостающих углов, лучше всего перестроить ее следующим образом:

cos(C) = a2 + b2 — c2 / 2ab и выполнять вычисления дальше. Помните, что закон косинусов не изменился в этом случае; мы просто изолируем переменную до того, как подключим всю необходимую информацию. Та же стратегия может быть использована для решения задачи для другого угла или другой стороны. Изолирование переменной вначале не меняет применения правила косинусов, оно просто облегчает правильное выполнение всех вычислений.