Треугольники SSS — это треугольники, у которых известны все три стороны. Внутренние углы могут быть неизвестны, но их можно определить, выполнив три действия. Понимание SSS-треугольников и способов решения для нахождения углов может быть полезно в различных ситуациях вне уроков математики, например, когда нужны точные углы для строительства чего-либо.
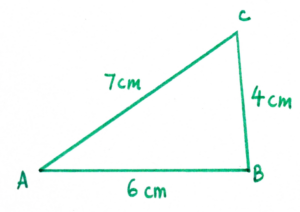
Основы треугольников
Треугольники имеют определенные правила, которые облегчают учащимся нахождение любого угла или стороны на основе того, что они уже знают. В треугольниках SSS три стороны уже известны, поэтому ученик может использовать приведенные ниже шаги для определения всех углов, чтобы решить треугольник. Благодаря этим основным правилам ученику достаточно знать одну формулу и способы ее перестановки для нахождения углов.
Три шага для нахождения углов треугольника SSS
Чтобы найти углы треугольника SSS, ученик должен выполнить три шага, по одному для каждого угла. Сначала нужно использовать закон косинусов для определения одного из углов. Обычно целесообразно сначала поработать с самым большим углом. Затем можно использовать закон косинусов для нахождения другого угла. Наконец, для нахождения третьего угла нужно сложить два первых и вычесть из 180.
Закон косинусов
Закон косинусов гласит, что c^2=a^2+b^2-2ab cos(C). Когда все числа подставлены, это можно использовать для сторон и углов треугольников. Однако для треугольника SSS его нужно использовать для нахождения первого угла, когда известны все три стороны. В этом случае полезно начать с немного измененной формулы. Для решения угла C сначала используйте формулу: cos(C)=(a^2+b^2-c^2)/2ab. Ее можно изменить, чтобы найти и другие углы.
Снова используйте закон косинусов
После того как первый угол найден, ученик может использовать тот же закон для нахождения второго угла. Для угла B нужно использовать формулу cos(B)=(c^2+a^2-b^2)/2ca. Чтобы решить угол A, нужно использовать формулу cos(A)=(b^2+a^2-c^2)/2bc. По сути, это те же формулы, что и в предыдущем шаге, но они были изменены, чтобы сделать их лучшей отправной точкой в зависимости от угла, который человек хочет решить. Их можно использовать в любом порядке, а закон косинусов нужно использовать только дважды.
Сложение и вычитание для последнего угла
Углы в треугольнике всегда складываются в 180 градусов, независимо от типа треугольника. Когда ученик знает два угла, он может сложить их вместе и вычесть из 180, чтобы определить последний угол. К этому моменту они будут знать все 3 стороны и все 3 угла треугольника.
Умение находить углы в треугольнике может быть полезно в самых разных ситуациях. Уделив время изучению закона косинусов и тому, как его можно перестроить, чтобы облегчить нахождение угла, ученик сможет решить любой треугольник SSS. Практикуйте несколько задач сегодня, чтобы получить немного больше опыта работы с треугольниками SSS уже сейчас.