Буквы ASA означают угол — сторона — угол, то есть треугольник с двумя известными углами и известной длиной одной стороны между двумя углами. Имея такую информацию, мы можем определить оставшийся угол и длину двух других сторон.
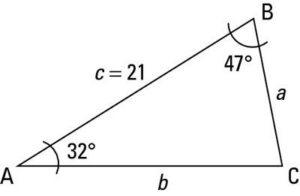
Нахождение третьего угла треугольника ASA
Представьте себе треугольник со сторонами a, b и c, где длина стороны a = 5 дюймов. Мы знаем, что угол между сторонами a и b равен 60 градусам. Мы знаем, что угол между сторонами a и c равен 90 градусам. Чтобы узнать третий угол, нам достаточно вспомнить правило, согласно которому сумма трех углов любого треугольника всегда равна 180. В данном примере 60 + 90 + ? = 180. Поскольку 60 + 90 = 150, а 180 — 150 = 30, мы знаем, что угол, где b пересекается с c, равен 30 градусам.
Нахождение двух оставшихся сторон треугольника ASA
Формула для нахождения сторон треугольника ASA немного сложнее и требует использования функции синуса на калькуляторе. Сначала изобразим треугольник, как показано выше, со сторонами a, b и c. Обозначим угол, противолежащий каждой стороне, заглавной буквой, так что угол, противолежащий стороне a, будет A, угол, противолежащий стороне b, — B, а угол, противолежащий стороне c, — C. Используя эти обозначения, закон синусов гласит, что
a/sin A = b/sin B = c/sin C
Поэтому, если нам известны хотя бы два угла и одна противоположная сторона, мы можем использовать формулу для нахождения длин двух других сторон.
В приведенном выше примере мы знаем, что одна сторона (a) имеет длину 5 дюймов, и знаем, что противоположный угол A (где b пересекается с c) равен 30 градусам. Мы также знаем, что угол B напротив стороны b равен 90 градусам. Мы можем использовать эту информацию для составления уравнения: 5/sin(30) = b/sin(90).
Используя алгебру, мы можем перестроить уравнение следующим образом
b = 5/sin(30) x sin(90)
b = 5/.5 x 1
b = 10 дюймов
Затем мы можем проделать то же самое со стороной c, зная, что ее противоположный угол C равен 60 градусам. Для вычисления c мы можем использовать либо a/sin(A), либо b/sin(B). Используя первую сторону и угол, a/sin(A), мы можем составить новое уравнение 5/sin(30) = c/sin(60). Переставив уравнение, мы можем решить его следующим образом.
c = 5/sin(30) x sin(60)
c = 5/.5 x .87
c = 8,7 дюйма
Практика
Задача: Учитывая следующие данные о треугольнике ASA, решите угол C и стороны a и b.
Угол A = 50 градусов
Угол B = 70 градусов
сторона c = 6 дюймов
Решение:
Чтобы найти третий угол, сложите A и B и вычтите из 180. Угол C равен 60 градусам.
Чтобы найти сторону a, используйте правило синуса: a/sin(50) = 6/sin(60)
a = 6/sin(60) x sin(50)
a = 6/.87 x .77
a = 5,3 дюйма
Чтобы найти сторону b, используйте правило синуса b/sin(70) = 6/sin(60)
b = 6/sin(60) x sin(70)
b = 6/.87 x .94
b = 6,5 дюйма