Треугольники

Треугольники — это двумерные фигуры, состоящие из трех сторон и трех углов. Хотя не все треугольники одинаковы, все они должны иметь эти два элемента, чтобы быть треугольником. Вы можете встретить несколько различных типов треугольников, каждый из которых определяется сторонами и/или углами.

Острый: В остроугольном треугольнике все три угла меньше 90 градусов.

Тупой: В тупоугольных треугольниках один угол больше 90 градусов.

Прямоугольный: Прямоугольный треугольник имеет один угол 90 градусов.

Равносторонний: Равносторонние треугольники имеют три равные стороны и три равных угла.

Масштабируемый: У масштабируемого треугольника нет равных сторон и углов.

Равнобедренный: У равнобедренных треугольников две равные стороны и два равных угла.

В любом треугольнике, независимо от его типа, все три угла равны 180 градусам. Вы можете использовать этот факт, чтобы найти измерение недостающих углов. Например:

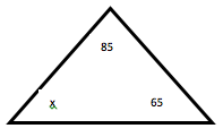
В этом треугольнике один угол равен 85 градусам, а другой — 65. Сумма трех углов должна равняться 180 градусам, поэтому:

85 + 65 + x = 180

150 + x = 180

150 — 150 + x = 180 — 150

X = 30

Геометрия также дает нам правила для нахождения площади треугольника. Формула для нахождения площади — это ½ основания, умноженная на высоту, или ½ x b x h = A. Основание — это нижний край треугольника, а высота — это вертикальная линия, проходящая от основания до противоположного угла в 90 градусов.

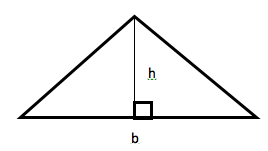
Допустим, основание (b) этого примера треугольника равно 72, а высота (h) — 50. Когда вы подставите эти числа в уравнение площади (A), оно будет выглядеть следующим образом:

½ x 72 x 50 = A

Затем, если вы продолжите решать задачу на нахождение площади, вы проделаете следующие шаги:

½ x 3 600 = A

A = 3 600 x 1/2

A = 1,800

Помните, сначала всегда умножайте основание на высоту. Затем умножьте это число на ½. Вы также можете представить это как деление b x h на два.

Конгруэнтность

Два треугольника считаются конгруэнтными, если их стороны и углы одинаковы. Неважно, перевернуты ли они боком, вверх ногами или являются зеркальным отражением друг друга: они все равно будут иметь одинаковые размеры. На протяжении веков было создано пять теорем о конгруэнтных треугольниках, и вы можете использовать их, чтобы выяснить, одинаковы ли два треугольника, или нарисовать треугольник, конгруэнтный тому, который уже есть на бумаге.

Сторона-сторона-сторона (SSS): Если все три стороны двух разных треугольников одинаковы, то их углы тоже будут одинаковыми, поэтому они конгруэнтны.

Сторона-угол-сторона (SAS): Если две стороны треугольника и угол, образованный при пересечении этих сторон, совпадают с углами другого треугольника, то треугольники конгруэнтны.

Угол-сторона-угол (ASA): если два угла и соединяющая их сторона в двух разных треугольниках имеют одинаковые размеры, то они конгруэнтны.

Угол-сторона-угол (AAS): Если два угла одного треугольника совпадают с двумя углами другого и одна сторона каждого из этих треугольников измеряется одинаково, можно быть уверенным, что они конгруэнтны.

Гипотенуза-нога (HL): Эта теорема применима только к правильным треугольникам, или треугольникам с одним углом 90 градусов. Если гипотенуза, или самая длинная сторона, и другая сторона двух треугольников имеют одинаковую длину, то треугольники конгруэнтны. Вы уже знаете, что углы, противолежащие гипотенузам, одинаковы.

Каждый раз, когда вы используете одно из этих правил для доказательства конгруэнтности двух треугольников или строите свою собственную модель конгруэнтного треугольника, вы можете быть уверены, что все стороны и углы, на которые не распространяется теорема, будут одинаковыми.

Треугольник — это, по сути, сумма его частей. Вы можете использовать эти части для построения одинаковых треугольников, подтвердить, что два треугольника уже одинаковы, или доказать, что они вовсе не одинаковы, как бы похожи они ни были. Отсутствующие углы не являются проблемой, потому что вы можете использовать те, которые у вас есть, чтобы найти тот, которого нет. Учитывая все вышесказанное, развлекайтесь с этими трехсторонними и трехугольными фигурами, и пусть вас не пугают недостающие углы!