Теорема Пифагора

Теорема Пифагора: Нахождение недостающей длины

Геометрия начала формироваться тысячи лет назад. Хотя к созданию этой отрасли математики приложили руку многие великие умы прошлого, о некоторых из них можно услышать больше, чем о других. Один из самых известных — Пифагор. Он был философом, учителем и талантливым математиком, и именно ему принадлежит одно из самых важных правил о правильных треугольниках, которое вы будете использовать в геометрии: теорема Пифагора.

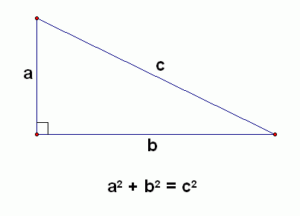
Теорема Пифагора звучит следующим образом: «Квадрат гипотенузы правильного треугольника равен сумме квадратов двух других сторон». Когда вы используете ее для нахождения гипотенузы, она будет записана так:

a2 + b2 = c2

В правильном треугольнике один угол всегда равен 90 градусам. Гипотенузой, или самой длинной стороной, будет та, которая лежит прямо напротив прямого угла. Когда вы используете теорему Пифагора, это всегда будет сторона «c». Какая из сторон в итоге окажется «a» или «b», не имеет значения, но сторона напротив прямого угла должна быть «c», иначе вы подставите себя под большое падение.

Учитывая все вышесказанное, давайте начнем с базового примера нахождения длины гипотенузы правильного треугольника.

Допустим, длина стороны «a» в нашем примере равна 12, а длина стороны «b» — 8. Наша задача — найти длину стороны «c», поэтому наша задача будет выглядеть следующим образом:

122 + 82 = c2

Мы должны возвести в квадрат стороны «a» и «b», или умножить их на себя, чтобы перейти к следующему шагу в уравнении:

144 + 64 = c2

Дальше мы просто складываем квадраты «a» и «b» вместе, чтобы приблизиться к нашей загадочной длине гипотенузы.

208 = c2, или c2 = 208

Поскольку 208 — это квадрат нашей гипотенузы, мы еще не закончили. Нам нужно найти квадратный корень из 208, то есть найти число, которое нужно умножить на само себя, чтобы получить 208. Если у вас под рукой есть научный калькулятор, вы можете ввести 208, нажать кнопку, похожую на стрелку вверх (^), и ввести .5. В качестве альтернативы можно нажать кнопку «2», а затем «x2». Затем введите 208 и нажмите клавишу «enter/=».

Если вы шифруете без помощи техники, то вам просто нужно найти два числа, которые при возведении в квадрат приближаются к 208, одно чуть ниже, а другое чуть выше. Так получилось, что 142 — это 195, а 152 — 225, поэтому:

c ≈ 14,5 по математике, или c ≈ 14,4 по калькулятору.

Вы также можете использовать теорему Пифагора для нахождения длины стороны «a» или «b», если вам уже известна длина гипотенузы. Все нужно просто немного переставить. Вот еще один пример:

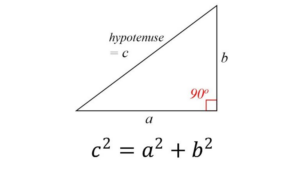
Допустим, мы уже знаем, что длина гипотенузы равна 12, а длина стороны «b» — 9. Начните с того, что напишите уравнение по теореме Пифагора, как обычно, вставив уже имеющиеся числа:

a2 + 92 = 122

В результате получится:

a2 + 81 = 144

Поскольку нам нужно уравновесить уравнение, чтобы получить «a», мы просто вычтем 81 из обеих сторон:

a2 + 81 — 81 = 144 — 81

a2 = 63

a ≈ 7.9

Считается, что Пифагор не разрешил записывать свои концепции, но его ученики передавали его учение другим. В конце концов, эта теорема стала достоянием общественности и дала нам возможность находить длину любой стороны правильного треугольника, если мы имеем представление о том, какими могут быть две другие стороны.