Как только вы попадаете в мир трехмерных фигур, математика начинает приобретать совершенно новый уровень глубины. Нахождение объема простых, обычных фигур может быть сложной задачей для некоторых, но когда вы начинаете наращивать их, процесс становится еще более сложным. Пирамиды — одни из самых известных 3D-фигур. Хотя вы найдете множество типов с любым количеством треугольных граней, мы пока сосредоточимся на прямоугольных пирамидах.
Нахождение объема прямоугольной пирамиды
Прямоугольные пирамиды имеют четырехгранные основания и четыре треугольные грани, сходящиеся в вершине, или, как ее еще называют, остроконечной вершине. Общая формула для нахождения объема этих многогранных форм — V = (l x w x h) / 3. По сути, первым шагом будет определение площади основания путем умножения длины на ширину.
Как только вы определите площадь основания, умножьте ее на высоту. Высота — это расстояние от центральной точки основания до вершины. После умножения площади основания на высоту разделите ответ на три, чтобы получить объем. Вот пример прямоугольной пирамиды и некоторые примеры измерений:
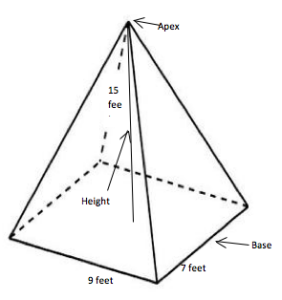
Начните с базовой формулы, подставьте данные измерений и действуйте осторожно.
V = (l x w x h) / 3
V = (9 x 7 x 15) / 3
V = (63 x 15) / 3
V = 945 / 3
V = 315 футов3
Вы также можете увидеть формулу в следующем виде: V = 1/3 Bh. Это означает, что вы просто умножаете основание на высоту и делите на три, что является одним и тем же процессом. Имейте в виду, что обе формулы работают и для квадратных пирамид, поскольку квадраты являются разновидностями прямоугольников.
В некоторых случаях вам может понадобиться определить высоту пирамиды, прежде чем вы сможете вычислить ее объем. Допустим, вам дана наклонная высота пирамиды, то есть расстояние от вершины до центра одной из треугольных граней. Это немного усложняет задачу, но далеко не исключает ее. Вот пример:
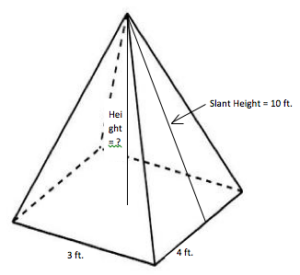
Помните, что линия, обозначающая высоту, проходит от вершины к центру основания и образует угол 90 градусов в основании пирамиды. Это делает треугольник, образованный высотой, наклонной высотой и основанием, правильным, поэтому вы можете использовать теорему Пифагора (a2 + b2 = c2), чтобы найти недостающее число. Гипотенуза, или сторона «c«, — это самая длинная сторона, которая всегда находится прямо напротив угла 90 градусов в правильном треугольнике.
Мы еще не знаем высоту, или сторону «a«. Поскольку базовое измерение, которое мы будем использовать здесь, равно трем футам, высота от центра до наклонной плоскости будет равна 1,5. Это будет сторона «b«. Вот процесс нахождения недостающей высоты:
a2 + b2 = c2
a2 + 1.52 = 102
a2 + 2.25 = 100
a2 + 2.25 — 2.25 = 100 — 2.25
a2 = 97.75
a ≈ 9.9
Зная, что высота вашей пирамиды почти равна 9,9, вы можете, как обычно, решить вопрос о ее объеме.
Учитывая измерения основания и высоты прямоугольной пирамиды, вы можете решить задачу для нахождения ее объема. Если у вас есть ее наклонная высота, но нет фактической высоты, позвольте Пифагору помочь вам, прежде чем пытаться решить «V«. Если вы развиваете свои навыки в геометрии или готовитесь к путешествию в Гизу, вы будете готовы найти объем любой прямоугольной пирамиды на вашем пути!