Всех существ на Земле объединяет некая общая связь. Это не сложный, глубоко спрятанный элемент или какая-то потусторонняя связь; это простая истина. Все мы в какой-то момент появляемся на свет, и все мы покидаем наше существование в другой момент.
Между этими точками начала и конца у каждого из нас есть свой собственный опыт. Некоторые из них мы разделяем с другими людьми, другие являются чисто внутренними, но все они так или иначе влияют на нас. Являются ли все эти события чисто случайными, или же за ними стоит какая-то рифма и причина?
Многие философы, учителя, математики и вообще люди, живущие жизнью, считают, что нет ничего случайного. Человек, родившийся в Италии более 800 лет назад, относится к этой категории. Его звали Леонардо Пизано Боголло, но сегодня мы знаем его как Фибоначчи. В юном возрасте он полюбил цифры, и эта страсть привела его к открытию, способному изменить взгляды людей на жизнь и окружающий мир.
Последовательность Фибоначчи оживает
Некоторые считают, что если присмотреться, то можно найти закономерность в чем угодно. Это вполне может быть правдой, но Фибоначчи смог извлечь конкретную закономерность из своих знаний о числах и доказать, что она может, по идее, продолжаться вечно. Он указал на последовательность Фибоначчи в своей первой книге «Liber abacci», где он поставил перед всеми математически обоснованную словесную задачу для размышления.
«Некий человек посадил пару кроликов в месте, окруженном стеной. Сколько пар кроликов может быть произведено от этой пары за год, если предполагается, что каждый месяц каждая пара порождает новую пару, от которой на второй месяц и далее становится продуктивной?».
Сейчас самое время сварить кофе и найти аспирин, потому что ваш мозг сейчас взорвется!
Итак, поехали! Фибоначчи рассудил, что кролики достигнут зрелости и спарятся примерно через месяц, поэтому по прошествии месяца у них останется только одна пара кроликов. Поскольку их период беременности также составляет месяц, второй месяц подошел к концу, а пара все еще была одна. Однако в конце третьего месяца появилась вторая пара. Самки кроликов должны рожать раз в месяц после первого помета, поэтому на четвертом месяце первая пара произвела на свет еще одного крольчонка.
Наступил пятый месяц, и первая пара снова размножилась, а вторая сделала то же самое. К этому моменту общее количество пар составляло пять. Короче говоря, в конце года в стенах жили 377 пар.
Немного глубже
Конечно, Фибоначчи сделал несколько довольно смелых прыжков, прежде чем предсказать плодотворность этой путаницы. Его сценарий вращался вокруг некоторых строго контролируемых условий. Например,
Каждый новый помет состоял из двух кроликов: самца и самки.
Все они были физически способны к воспроизводству
Каждая самка была способна начать репродуктивный процесс в возрасте одного месяца и рожать новый помет каждый месяц.
Все они прожили целый год, не заболев и не будучи изгнанными из комплекса другими кроликами.
На самом деле, некоторым кроликам может потребоваться четыре месяца или больше, чтобы достичь зрелости. В одном помете может родиться до 12 потомков, и не все из них гарантированно выживут. Однако, если задуматься, неконтролируемое число и естественный отбор могут компенсировать друг друга. Хорошо продуманные условия Фибоначчи могли бы легко учесть все возможности и уравновесить весы.
Разбивка на части
В письменном виде все эти идеи могут звучать несколько абстрактно. Конечно, математика Фибоначчи точна. Но если поставить цифры на место слов, все становится немного понятнее. Последовательность Фибоначчи начинается с 0 и 1, а затем идет дальше. Проще говоря, это выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и так далее.
Каждое новое число в последовательности образуется путем сложения двух предыдущих чисел.
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
13+21=34
21+34=55
34+55=89
Можно продолжать до бесконечности, складывая два последних числа в последовательности, чтобы узнать следующее. Хотя объяснение звучит затянуто и сложно, на самом деле оно довольно простое. Однако с этого момента все становится гораздо сложнее.
Концепция обретает форму
Сейчас мы перейдем на совершенно новый уровень. Представьте, что числа в последовательности Фибоначчи представлены в виде квадратов, как на листе бумаги. Найдите начальную точку в центре листа и закрасьте один квадрат, представляющий первое число в последовательности (1). Рядом с ним сделайте то же самое в честь второго числа. Затем, поскольку два — это третье число, используйте другой цвет, чтобы заштриховать квадрат размером 2 на 2. Затем найдите другой оттенок для окрашивания пространства размером 3 на 3 квадрата и так далее. В итоге у вас получится яркая версия этого примера:
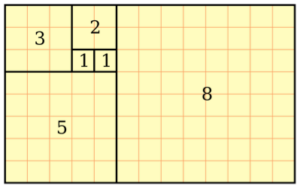
Вы заметили, как они идеально подходят друг к другу, как кусочки головоломки? Следующее число в серии — 13, и фигура, которая здесь вырисовывается, имеет размер 13 квадратов в поперечнике. По мере того как вы будете переходить к более крупным числам, схема останется неизменной. Каждый новый квадрат будет больше предыдущего, но, следуя числам в последовательности Фибоначчи, они всегда будут аккуратно вставать на место в точном соотношении с предыдущими.
Теперь, если вы работаете на бумаге, возьмите ручку. Начните с верхнего угла первого одиночного квадрата и нарисуйте первый этап спирали, идущей к противоположному углу, разрезая квадрат пополам. Продолжите линию через следующий одиночный квадрат и далее через следующие, проводя спираль по диагонали через центр каждого большого квадрата. В итоге у вас получится что-то вроде этого:

Спираль Фибоначчи и прямоугольник, созданный его последовательностью чисел, известны как Золотой прямоугольник из-за их связи с золотым сечением. В виде числа эта магическая цифра равна 1,61803 и обозначается греческой буквой Phi (Φ). Может показаться, что мы немного перескакиваем с одного на другое, но все это действительно имеет значение.
В геометрии золотое сечение создается, когда вы делите линию на две части, но не просто на две части. Линия должна быть разделена именно в том месте, где вся линия, разделенная на длину самой длинной части, в точности равна самому длинному отрезку, разделенному на самый короткий. Вы угадали: обе цифры должны быть равны 1,61803.
Считается, что прямоугольники, созданные с использованием золотого сечения, являются самыми приятными из всех, которые вы когда-либо видели. Это возвращает нас к Фибоначчи. Оказывается, когда вы берете любые два последовательных числа в его последовательности и находите их соотношение путем деления большего числа на меньшее, оно оказывается чрезвычайно близким к древнему золотому стандарту. Смотрите!
21/13 = 1.61538
89/55 = 1.47272
121393/75025 = 1.61803
Посмотрите на это! Мы нашли победителя! Последовательность Фибоначчи, золотой прямоугольник и присущая ему спираль — все это вокруг нас. Вы находитесь на пороге того, чтобы узнать, как и где.
Спираль в полный контроль
Прежде чем читать дальше, вам необходимо убедиться, что вы готовы совершить этот прыжок. Это всего лишь небольшой дружеский совет. Увидев это однажды, вы уже не сможете этого не увидеть, и это изменит вашу жизнь!
Золотой прямоугольник, созданный последовательностью Фибоначчи, появляется по всему миру на протяжении веков. Одним из ярких примеров является Парфенон в Греции. Многочисленные примеры золотого сечения и прямоугольника встречаются как в больших, так и в малых масштабах.
Мона Лиза Леонардо да Винчи может считаться еще одним проявлением почти золотого сечения в работе. Ее размеры, как говорят, составляют 30 на 21 дюйм. Если следовать стандартному плану, то большая сторона прямоугольника, деленная на меньшую, равна 1,42857. Это не точное совпадение, но близкое.
Отправляясь в Египет, мы находим еще один возможный пример в Великой пирамиде Гизы. Самая большая из трех пирамид, она имеет размеры 756 футов в ширину и 481 фут в высоту. Если посчитать, то соотношение составляет 1,57172; опять же, это прямо на пограничной линии.
Художник Пит Мондриан также вставлял последовательность Фибоначчи в некоторые свои картины. На некоторых его работах можно отчетливо увидеть квадраты-головоломки, составляющие «золотой прямоугольник». Если смотреть на картину достаточно долго, то ваш ум может даже начать рисовать спираль.
Это лишь несколько широко известных случаев использования этого узора в искусстве, архитектуре и технике на протяжении веков. Многие люди настаивают на том, что это простое совпадение, ссылаясь на то, что узоры можно найти практически во всем, если их искать. При этом некоторые из них появились задолго до самого Фибоначчи.
Многие объясняют это очевидным. За созданием этих произведений стоят одни из самых ярких и эстетически настроенных умов в истории. Чистая логика подсказывает, что они включили бы в свою работу наиболее визуально приятные размеры, даже если это происходит на подсознательном уровне.
Вы можете рационализировать ситуацию любым количеством различных способов, но все еще глубже. Некоторые вещи нельзя игнорировать или объяснять.
Это естественно
Если вы выйдете на улицу и посмотрите вокруг, то обнаружите Фибоначчи и в природе, причем не только в одном или двух разных местах. Подсолнухи — яркий тому пример. Эти блестящие желтые лепестки окружают большую массу семян, но семена расположены не бессистемно, они изящно выходят из центра семенной головки.
Сосновые шишки — еще один широко распространенный пример. Вы заметите, что их шишки расположены по спирали как по часовой, так и против часовой стрелки. То же самое можно сказать и об ананасах. Если у вас поблизости есть куст остролиста или другой подобный кустарник, посмотрите на него. Сначала кажется, что листья растут беспорядочно или даже по кругу. При ближайшем рассмотрении вы увидите, что на самом деле они расположены в шахматном порядке и идут неровными спиралями от верхушки к стволу.
Человечество также демонстрирует небольшие фрагменты «Золотого прямоугольника». Средние лица взрослых людей имеют размеры восемь-девять дюймов в длину и шесть-семь дюймов в ширину. Если вычислить соотношение двух крайних величин, то получится 1,5, то есть в пределах доли золотого сечения. Человеческие волосы имеют тенденцию расти наружу по спирали от центральной точки. Начиная с этого момента, вы начнете видеть варианты этой последовательности везде, куда бы вы ни посмотрели. Не говорите, что мы не предупреждали вас заранее!
Занимаемся математикой
Как и в большинстве математических ситуаций, в этой серии существуют правила подсчета чисел. В комплекте с ним идет множество формул. Прежде всего, давайте рассмотрим демонстрацию общего правила, связанного с последовательностью Фибоначчи:
xn = xn-1 + xn-2
Здесь «n» дает каждому числу в серии Фибоначчи соответствующее число в нашей традиционной последовательности: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
«Xn» представляет числа в последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Используя правило, мы можем вычислить число в последовательности. Попробуем вычислить седьмое:
x7 = x7-1 + x7-2
x7 = x6 + x5
x7 = 8 + 5
x7 = 13
На самом деле это просто другой способ сказать: «Определенное число в последовательности Фибоначчи равно сумме двух предыдущих чисел».
Дальше все становится только сложнее и сложнее. Вы найдете любое количество уравнений и объяснений, связанных с математической индукцией, линейным повторением, построением последовательности на графиках и т.д.
Эти формулы, простите за каламбур, являются греческими для тех, кто пытается с головой окунуться в продвинутую часть спектра. Если вы не обладаете некоторыми знаниями о реальных методах решения проблем, лучше всего облегчить себе задачу. Как только вы поймете основы, такие как приведенная выше формула, дальше все будет просто: делайте детские шаги.
В целом
У всех нас есть общие связи. Являются ли они случайными и совпадающими или продуктами математических последовательностей и таинственно упорядоченного хаоса — это в основном вопрос мнения. Независимо от вашей позиции по этому вопросу, определенные закономерности нельзя игнорировать или легко отбросить. Фибоначчи увидел это еще в детстве, и дело всей его жизни положило начало неудержимой последовательности событий.