Площадь

В математике геометрия — это наука о нахождении размеров фигур. Существует несколько различных измерений, которые можно вычислить в зависимости от типа фигуры. Эти измерения называются размерами. Ширина, глубина или высота являются примерами размеров.

Фигуры можно разделить на плоскости, геометрические фигуры или даже просто точки. Плоскости имеют только два измерения, такие как длина и ширина. Трехмерные фигуры имеют длину, ширину и высоту. Точка имеет только одно измерение. Если точка не занимает достаточно места для вычислений, то плоскости и геометрические фигуры занимают достаточно места. Это означает, что плоскости и геометрические фигуры имеют площадь, которую можно вычислить.

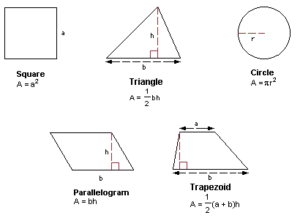
Для каждой фигуры существует своя формула для нахождения ее площади. Трехмерные фигуры имеют площадь поверхности, поскольку пространство внутри них нужно вычислять по-другому. Площадь внутри трехмерной фигуры называется объемом. Поскольку вычисление трех измерений намного сложнее, проще сначала сосредоточиться на изучении того, как находить площади двумерных фигур.

Размеры плоских фигур

Двумерная фигура не имеет объема, поэтому вычислить площадь внутри такой фигуры гораздо проще. В зависимости от типа фигуры эти размеры имеют разные названия, чтобы различать их и не путаться при измерениях. Например, у квадрата есть длина и ширина, а у треугольника — длина основания и перпендикулярная высота.

Чтобы внести ясность при измерении менее обычных фигур, углы по периметру фигуры также имеют названия. Правильный треугольник имеет прямой угол, изогнутый треугольник имеет восходящий и нисходящий углы.

Измерение площадей

Измерения по внешней стороне фигуры производятся в обычных единицах. Однако площадь измеряется в квадратных единицах, чтобы учесть объем. Обычные единицы измеряют только по прямой линии, квадратные единицы измеряют площадь. Возвести единицу измерения в квадрат очень просто, нужно лишь умножить ее на саму себя.

Квадраты считаются самой простой формой, поэтому у них самая простая формула — S2. Переменная S означает измерение одной стороны. Таким образом, площадь квадрата можно найти, измерив одну сторону и умножив ее на себя. Если сторона квадрата равна пяти сантиметрам, то его площадь равна двадцати пяти квадратным сантиметрам.

Несмотря на то, что прямоугольник также имеет ровные стороны, формула его площади отличается. Умножив длину и ширину, вы получите площадь прямоугольника.

Измерение площади криволинейных форм немного отличается. Для неправильных форм, таких как газон, можно создать контрольные точки. Для этого нужно найти самые широкие точки фигуры и провести измерения до противоположной стороны. Измерение между ними называется отрезком линии. Эти линии могут иметь определенные названия. Например, линия, которая проходит только половину пути, называется радиусом. Этот отрезок линии можно использовать для нахождения других измерений окружности. Диаметр определяется путем умножения радиуса на два.

При измерении площади изогнутых фигур в формуле, скорее всего, будет использоваться число Пи. Для нахождения площади круга используется формула 2x Pi x радиус. При радиусе четыре сантиметра формула будет 2x 3,14 x 4 с решением 25,12 квадратных сантиметров.

Для каждой уникальной формы необходимо использовать формулу для нахождения ее площади. Существуют десятки формул для нахождения площади, и каждая из них может быть по-своему полезна.

Найдя правильную формулу, можно легко найти решение реальных проблем.