Многоугольник

В математике каждая фигура имеет название, которое отличает ее от других фигур. Вместо просто треугольников существует несколько типов треугольников. Например, равносторонний треугольник отличается от скаленого треугольника. Существуют названия и для типов фигур. Любая фигура с тремя или более плоскими сторонами и углами называется многоугольником.

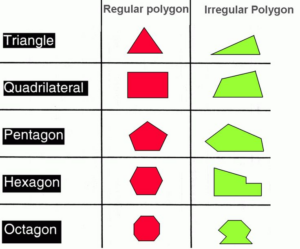
Многоугольники — это плоские фигуры, у них есть только ширина и длина. Слово многоугольник происходит от корня слов poly, что означает много, и gon, что означает стороны.

Многоугольники отличаются друг от друга, но все они подпадают под одно и то же определение. Все многоугольники — это двумерные фигуры с плоскими сторонами, состоящие из прямых линий, которые образуют замкнутую форму.

У правильных многоугольников стороны равны, у неправильных многоугольников одни стороны длиннее других.

Они также могут быть вогнутыми или выпуклыми, простыми или сложными. У каждого из этих типов многоугольников есть определение, которое отличает их от других фигур. Существует исчерпывающий список названий и определений многоугольников.

Измерение многоугольников

Многоугольники могут показаться сложным видом фигур, но это не так. Формулы для нахождения площади многоугольника просты и требуют решения только базовых математических задач. Например, для измерения периметра правильного многоугольника достаточно найти длину одной стороны и умножить ее на количество сторон.

Найдя апофему фигуры, можно получить формулу для вычисления площади. Апофема — это измерение от центра до одной из сторон многоугольника. Радиус можно найти, измерив расстояние от центра до угла или вершины.

Формула для нахождения площади правильного многоугольника — A = ½ периметра x апофема.

Подставив измерения пятиугольника со сторонами размером восемь дюймов, вы получите площадь. Периметр 40 и апофема 8 выглядят следующим образом: A = 1/2 (40 x 8). Площадь многоугольника будет равна 160. Для решения задач по неправильным многоугольникам и более сложным формам потребуются другие формулы, но действуют те же принципы.

Неправильные и сложные многоугольники

В отличие от правильных многоугольников, сложные и неправильные многоугольники не имеют сторон одинаковой длины. Это означает, что измерение одной стороны и умножение ее длины на количество сторон не даст периметра.

Для неправильных многоугольников начните с измерения длины всех сторон. Найдя сумму длин и разделив ее на количество сторон, вы получите длину стороны.

Длину стороны можно использовать для расчета периметра, умножив ее на количество сторон. Если длина стороны равна 8 дюймам, а сторон 5, периметр будет равен 40.

Сложные многоугольники можно решать аналогичным образом, но для этого необходимо выполнить несколько дополнительных действий. Линии, составляющие сложный многоугольник, часто пересекаются и создают несколько других фигур. Эти дополнительные фигуры необходимо разделить и измерить.

Преобразуя измерения неправильных и сложных многоугольников, можно решить задачу с помощью простых формул.

Чтобы найти апофему любого из периметров, полученные данные нужно подставить в форму правильного многоугольника. Периметр можно разделить на количество сторон, чтобы найти длину стороны соответствующей правильной фигуры, например пятиугольника. Формулы, использованные для нахождения апофемы и площади фигуры, теперь можно использовать для решения измерений неправильного или сложного многоугольника.