Линейное программирование

Линейные функции — это визуальное представление значений, которые создают прямую линию. Используя соответствующее уравнение для построения графика линии, можно представить значения с течением времени. Затем эти значения могут быть использованы для поиска дополнительной информации и решения проблем. Линейное программирование — это процесс построения графиков наборов данных вместе, чтобы найти максимальную и минимальную выгоду.

Такое решение может быть использовано в бизнесе для расчета оптимального объема инвестиций в сравнении с оптимальной производительностью для получения оптимальной прибыли. И наоборот, та же информация может быть использована для поиска минимальной производительности, чтобы показать прибыль.

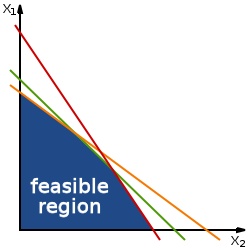
Построение графиков неравенств

Цель линейного программирования — обеспечить визуальную основу для неравенств. Эти неравенства отображаются на графике для оптимизации входа и выхода.

При построении графиков линейных функций данные могут быть представлены в виде визуального представления либо входа, либо выхода. Однако вариации данных подчиняются критериям, которые невозможно отобразить с помощью линейных функций. Это означает, что требуется другой тип решения проблемы.

Графики линейных функций могут отображать известные данные, а также могут быть использованы для отображения неравенств, которые обеспечивают контрастность известных переменных. Это называется линейными отношениями. Уравнения, используемые для максимизации, поиска вариаций и оптимизации, обманчиво просты.

Математическая оптимизация

Эти три уравнения имеют совершенно разные функции, но в них используются одни и те же данные. Уравнение для максимизации использует c для представления известных векторов коэффициентов и x для представления переменных векторов коэффициентов. Функция ( . ) T используется для переворачивания матрицы по диагонали, чтобы ее было легче представить на графике.

Неравенства, или ограничения, представлены в виде Ax ≤ b и x ≥ 0. Комбинация функций maximize и subject to образует область выполнимости, или область, в которую должен попасть вход или выход, чтобы оптимизировать известные данные.

Примеры оптимизации

Если фермеру необходимо посадить два вида культур и получить прибыль, ему нужно рассчитать стоимость удобрений на квадратный километр, стоимость пестицидов на квадратный километр и цену продажи обеих культур. Переменные в задаче должны быть представлены как F — удобрения, P — пестициды, S — цена продажи и L — земля. Приращения этих переменных будут представлены квадратными километрами.

Каждый километр, или x, одной культуры требует F1 и P1. Второй вид культуры потребует F2 и P2 на х2.

Первым шагом будет максимизация дохода с помощью уравнения S1 * x1 + S2 * x2 = Доход. Далее необходимо рассчитать ограничения. x1 + x2 < L представляет собой предел общей площади, доступной для посадки. F1 * x1 + F2 * x2 < F представляет собой предел удобрений, или F. P1 * x1 + P2 * x2 < P представляет собой предел пестицидов. Наконец, x1 > 0, x2 > 0 представляет ограничение, согласно которому культуры не могут быть посажены на отрицательной площади.

Эта информация может быть использована для формирования матрицы, которая затем может быть использована для расчета дохода, полученного от продажи урожая. С помощью этого алгоритма фермер сможет прогнозировать прибыль и затраты, что позволит ему оптимизировать усилия, чтобы заработать достаточно денег к концу сезона.