Круг

Свойства кругов

Все знают, что такое круг. Мы видим их каждый день по всему миру. Но мы можем не замечать, насколько важны круги и как отличительные свойства круга делают его полезным в самых разных отношениях. Чтобы понять, как эта уникальная форма может быть использована для решения задач и понимания окружающего мира, важно понять свойства круга.

Круг определяется как фигура с равным расстоянием до всех точек от ее центра. Углы отсутствуют, таким образом, образуя круглую форму. Чтобы отличить круги друг от друга, их можно назвать по точке в центре.

Круги бывают любого размера, и их можно различать, определяя площадь и поперечное сечение.

Площадь круга

Радиус, диаметр и окружность определяют площадь круга. Окружность — это площадь внешней стороны круга, и ее можно найти, только определив диаметр и радиус круга. Радиус находится путем измерения от центра к внешней стороне, а диаметр — путем измерения расстояния через середину, или с помощью уравнения R x 2 = D

Окружность найти немного сложнее. Во-первых, важно понять число Пи. Для базовых математических задач Pi имеет значение 3,14. Однако полное значение числа Пи еще не определено, поскольку считается, что это бесконечное число. Чтобы найти окружность круга, необходимо воспользоваться уравнением 2π x R = C.

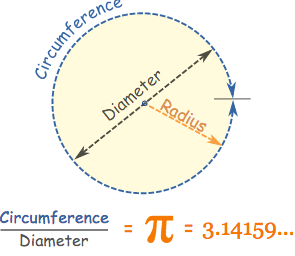
Должно быть ясно, что радиус окружности является самым важным измерением. Нахождение этого измерения позволяет определить любое другое геометрическое свойство окружности с помощью правильного уравнения. Это подтверждается и в дальнейшем, когда мы пытаемся найти площадь круга. Площадь находится с помощью уравненияπ x R2.

Поперечные линии круга

Поскольку окружности представляют собой группу точек, находящихся на одинаковом расстоянии друг от друга и исходящих из центральной точки, можно определить углы и прямые внутри окружности. Эти линии называются поперечные линии. Чтобы было понятно, поперечная линия определяется как линия, которая пересекает две или более прямых и может существовать внутри окружности или использоваться для нахождения окружности.

Поперечные линии используются для измерения и определения углов внутри ряда линий. Измеряя эти углы, можно найти геометрические параметры круга.

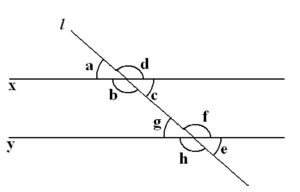
Круг — это триста шестьдесят градусов, полукруг — сто восемьдесят градусов. Измерение углов, образованных пересекающимися пересекающимися линиями, всегда дает круг, но пересечение не обязательно должно находиться в центре круга.

В качестве альтернативы можно построить поперечные линии, чтобы найти площадь определенного участка круга.

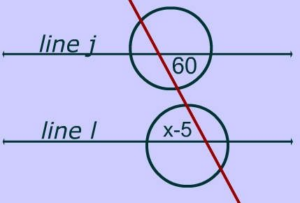
Найдя поперечные линии и измерив углы, можно найти и измерить окружность. Проще говоря, пересекающиеся линии измеряются для определения геометрии круга. Существует три набора углов, которые можно измерить. Соответствующие углы находятся на одних и тех же участках линий. Альтернативные внутренние углы находятся на противоположных участках линий между двумя прямыми. Альтернативные внешние углы лежат на противоположных областях вне прямых.

Измерение этих углов доказывает существование круга и может быть использовано для нахождения всех геометрических аспектов этого круга путем использования соответствующих данных в правильном уравнении после измерения радиуса.