Приходилось ли вам писать что-то и случайно добавлять или опускать запятую или другой знак препинания? Если да, то вы наверняка заметили, как это изменило смысл написанного. Классический пример с бабушкой демонстрирует огромное влияние мельчайших знаков препинания:
«Давай поедим, бабушка!».
против
«Давай поедим, бабушка!».
Неправильная пунктуация приводит к изменению смысла и ошибкам.
Математика тоже имеет уникальную систему пунктуации. Это также система, в которой точность имеет первостепенное значение. В математике неправильно поставленная запятая может означать разницу между банкротством и изобилием! Как и в языке, неправильное использование пунктуации в математике приводит к ошибкам.
Если грамматика математики — это формулы, уравнения и т.п., то пунктуация — это ее обозначения. Как точка является первым пунктуационным знаком в письменной речи, так и интервальные обозначения являются основой ясного математического смысла. Интервальные обозначения точно передают определенный диапазон математических возможностей.
Каждый числовой диапазон имеет начальную и конечную точки. Числа между ними, которые могут включать или не включать эти точки, называются множеством. Интервал — это множество, представляющее вещественные числа между первой и последней цифрами.
Возможно, вы хотите обозначить набор чисел в текущем месяце до вашего дня рождения включительно. Возможно, вы хотите обозначить все числа, превышающие 5. Возможно, вы захотите записать числа, меньшие или равные 20. Независимо от числового содержания данного набора, его можно передать с помощью интервальной нотации.
Самый простой способ представить интервал — это числовая линия.
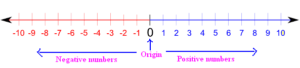
Чтобы обозначить интервал от -4 до 3, закрасьте пространство над линией, которая простирается между -4 и 3. Вы также должны сообщить, входят ли -4 и 3 в указанный интервал. Для этого нарисуйте круги на засечках, обозначающие соответствующие числа. Открытый круг означает, что число находится вне интервала. Замкнутый (цветной) круг указывает на включение. Интервал считается замкнутым, если обе конечные точки являются его членами.
Однако числовая линия — не единственный способ математически изобразить этот интервал. Существует довольно много способов сказать то же самое. Если бы числовая линия изображала набор значений, возможных для переменной x, вы могли бы добиться того же эффекта, написав:
-4 ≤ x ≤ 3
Альтернативный способ выразить этот интервал следующий:
[-4, 3]
Скобки указывают на то, что ближайшее к каждой скобке число находится внутри интервала. Парентеза вместо скобки указывает на исключение.
Другой способ обозначить интервал:
{x ε R | -4 ≤ x ≤ 3}.
В переводе это означает: «Множество x, входящих в набор действительных чисел, таких, что -4 меньше или равно x, меньше или равно 3».
Опять же, можно написать:
X ε R | x ε [-4, 3].
Обозначайте свой интервал как угодно, но помните об одном: если вы ошибетесь хотя бы в одной маленькой части математической пунктуации, вы, скорее всего, измените смысл всей задачи!