Асимптоты

Асимптоты используются для помощи студентам при построении графиков рациональных функций. Существует три различных вида, но наиболее распространенными и простыми для понимания являются горизонтальная и вертикальная асимптоты, поэтому начнем с них. Асимптота определяется как линия, к которой приближается кривая по мере приближения к бесконечности. Направление этих линий может быть как положительным, так и отрицательным, но для того, чтобы считаться асимптотой, расстояние между линией и кривой должно стремиться к нулю.

Как подразумевается, горизонтальная асимптота функционирует на горизонтальной оси, или оси «x».

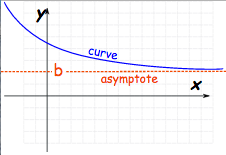
Вертикальная асимптота функционирует на оси «y».

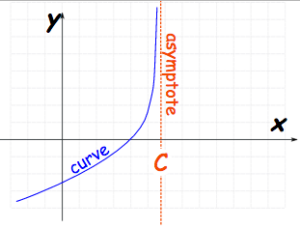
Третий вид асимптоты называется косой асимптотой. Вместо того чтобы зеркально отражать ось «x» или «y», косые асимптоты следуют формуле «y=mx+b» по мере приближения «x» к бесконечности

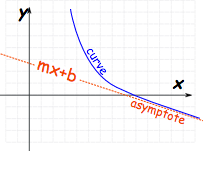
Это немного сложнее, верно?

Вероятно, пришло время потратить несколько минут на то, чтобы оценить применение асимптот всех видов. Как отмечалось выше, они полезны при построении графиков рациональных выражений. Рациональное выражение выражает отношение между многочленами. Оно похоже на дробь, только с многочленами. Как и обычная дробь, рациональное выражение содержит числитель и знаменатель. Вот пример: f(x) = (x2-3x)/(2x-2). И числитель, и знаменатель этого выражения содержат многочлены, что делает его рациональным выражением.

Теперь, когда эти выражения визуально представлены на графике, они могут иметь любое количество вертикальных асимптот. Однако у них может быть только одна или ноль горизонтальных и наклонных асимптот. Первый шаг, который необходимо сделать для нахождения значения любой асимптоты, — это сократить выражение до его младших членов. Следующий шаг будет зависеть от того, какой тип асимптоты пытается найти ученик.

Нахождение горизонтальных асимптот

В случае горизонтальных и косых асимптот они определяются на основе степени нижнего многочлена по сравнению с верхним. Если верхняя степень меньше нижней, то горизонтальная асимптота будет в нуле. Это довольно просто. Если они равны, то асимптота будет задана ведущими членами каждого полинома. Поскольку все может оказаться немного сложнее, рассмотрим другой пример: f(x) = (3x+1)/(4x+1). Независимо от значения «x», асимптота может быть определена через ¾, поскольку это ведущие члены многочлена.

В случаях, когда степень верхнего многочлена на 1 больше, чем нижнего, получается косая асимптота. Для нахождения уравнения линии необходимо использовать длинное деление многочлена, что лучше оставить для другого урока. Если степень верхнего многочлена больше степени нижнего более чем на 1 градус, то горизонтальной или наклонной асимптоты просто не существует.

Нахождение вертикальных асимптот

Вертикальные асимптоты возникают, когда нижний многочлен в рациональном выражении равен нулю. Например: f(x) = (x2-3x)/(2x-2). Поскольку вертикальная асимптота зависит только от знаменателя, мы сосредоточимся именно на нем: (2x-2) умножается на 2(x-1), что ставит вертикальную асимптоту при x=1, так как 1-1=0.

Понимание асимптот и рациональных функций, конечно, может быть сложной задачей, но достаточно практики с графическим калькулятором, и со временем это будет легко!